これは一見、つじつまが合わないように思えるかもしれないけど、フラットランドではすべてがまっすぐな線に見えると前に言ったよね。
必然的に、視覚によって階級のちがいを判別することはできないとも言った。
ところが、これから私のスペースランドではどのように視覚でお互いを認識するのか、について解説していこうと思う。
前の触覚による判別を読み返してもらえれば、「低位階級では」とあるのを見つけることができるはず。お互いを目で判別するのは、温暖な地域に住む高位階級の間でのみ可能なことなのさ。
どこの地域でも、どこの階級でも、霧があることによってこのような方法でお互いを判断することができる。この霧は熱帯地域を除く、すべての場所でほぼ1年中にわたって存在している。あなたのスペースランドにとっては、風景を遮る霧は憂鬱で不健康なものだろうけど。私たちにとっては自然の恵み、芸術の乳母、科学の親とされている。どういうことかというとね。
もし、霧が存在しないとしたら、どの線もはっきりと同じように見えるだろう。実際に空氣が乾いた国ではね、どの線も区別できない。しかし、霧がたくさんあれば、離れたところ、例えば1メートル先のものは50センチほど先のものよりも、かなりぼやっとして見える。その結果、暗さや鮮明さを注意深く比べることによって、目に見えるものの形をかなり正確に予測できるようになるのだ。
あれこれ説明するよりも、ひとつ例をあげた方がいいだろうね。
今、目の前にふたりの人が近づいてきたとする。私が彼らの階級を見分けようとしている。そしてそれぞれ仮に、商人と医者、つまり、三角形と五角形だったとしよう。どうやって見分けることができるだろうか?
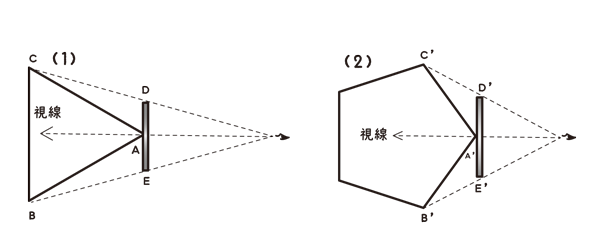
スペースランドの子どもたちにも、この幾何学の仕組みをご理解いただけるだろう。近づいてきた図形の角Aの方から見ると、こちらからは2つの辺、CAとABが均等に、同じ長さに見えるだろう。これは(1)も(2)も同じはず。
ここで相手が三角形の商人(1)だとしたら、どんなふうに見えるかな。私の目にはきっと、直線DAEが見えて、さらにその中点Aはとても明るく見えるはずだ。なぜなら、その点が私の目にもっとも近いからね。そして、その両側は急に暗くなっていく。なぜなら、辺ACと辺ABは霧の奥へかなり突っ込まれているからで、商人の両端、つまりDとEはかなり暗く見えることになる。
一方、医者の場合は(2)になる。この場合でも1本の線D’A’E’、中央の明るい点A’が見えるけど、両端はそれほど急に暗くなってはいない。なぜなら、この2つの辺、A’C’とA’B’はそれほど急に霧の中へ入っていないからで、医者の両端D’とE’は商人の両端ほどは暗くはならない。
この例でわかってくれただろうか。長年の訓練と経験によって、私たちの教養ある階級では、かなり正確に低位階級と中間階級とを正確に見分けることができる。スペースランドでは信じられない話でも、否定しないでそういうこともあるかもな、と理解してくれたならいいけど。これについてもっと詳しく話そうと思っても、視覚の認識は複雑で繊細なもので、どうやって説明したらよいかわからないな。
たとえば、私の父親である三角形が近づいてきたとする。
父がこちらに辺を向けていればだよ、向きを変えるよう頼むか、私がぐるりと回ってみるまで、それが直線、つまりご婦人である可能性を否定できないのさ。
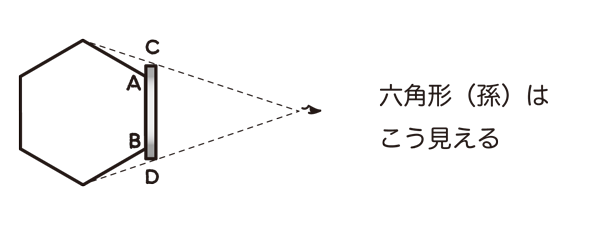
あるいは、ふたりの六角形の孫と一緒にいて、孫の辺ABを正面からながめたとする。するとね、この図からもわかるように、私の目にはとても明るい線、端まで明るさが変わらないまっすぐな線がひとつ。さらに2本の短い線、CAとBDが全体的には暗く、両端のCやDに向かってさらに暗くなっているように見える。
しかし、これ以上この話は続けない方がいいだろうね。
スペースランドの数学者たちにすら、この世界の舞踏会や座談会で図形がバラバラに回ったり前後に動く中、その多角形たちを正確に見分けることは難しい。これは最高の知性をもつ、ウェントブリッジ大学の静止幾何学か運動幾何学の教授たちくらいの資質がなければ不可能だ。かのウェントブリッジ大学では、大勢のエリート向けに視覚認識講座が定期的に開かれているくらいさ。
この貴重な技術を深く探求できるのは、時間と資産ある裕福な若者ほんのわずか。私もけして卑しい身分ではないし、非常に有望かつ完璧な正六角形の孫を2人も持つ私ですら、くるくると回転する多角形に囲まれて困惑することがある。ましてや普通の商人や奴隷にとってこのような光景は理解不能、あなたが突然こちらの世界に連れてこられたような状況だろう。
人混みの中では、どちらを向いても線ばかり。部分的、不規則的に明るかったり、暗くなったりしているまっすぐな線が見える。たとえ大学の五角形や六角形のクラスで3年間学んでも、この分野の理論を完全に理解していたとしても、実際の認識は難しいもの。
高位階級社会の人混みを身分の高い人にぶつからないように歩くためには、何年もの経験が必要だ。高位階級の図形にふれるのは礼儀に反することだし、あちらは教養があってこちらの動きを熟知しているのに、こちらは相手の動きをほとんど、いや、まったく知らないわけだから。つまり、多角形社会で完璧な礼儀作法を身につけるためには、本人が多角形階級でなくてはならないのさ。少なくとも私は、長く苦い経験からこの結論にいたったね。
驚くべき視覚認識の技術、本能というものは「ふれる」ことを避ける日頃の実践によって開発されている。小さい頃から「ふれる」ことに頼ってしまうと、「見る」のを完璧に習得することは難しい。そんな理由もあって、高位階級では「ふれる」ことは避けられたり、完全に禁止されたりする。ゆりかごから出た子どもたちは、ふれる技術を教える公共の学校ではなく、特別な学生しか入ることのできないより高級な学校へ通う。ある著名な大学では「ふれる」のはもっとも深刻な失敗とみなされ、1回の違反で停学となり、2回目には退学となってしまう。
低位階級の者にとって、目による認識は手の届くことのない、贅沢品さ。単なる商人には、息子の人生の3分の1を観念的な学習のために費やす余裕はない。そのため、貧しい者の子どもたちは早い時期から「ふれる」ようになり、彼らは早熟で活発になっていく。これは多角形階級の若者たちが不活発で未成熟であることと対照的なようだが、ひとたび大学を卒業して理論を実践しはじめたら、これはもう新しい誕生といってもいいような劇的変化が起きる。彼らは芸術や科学、社会活動などすべての分野で競争相手の三角形を追い越し差を広げていく。
大学の最終試験に落ちる多角形階級の生徒はごくわずかだ。しかし、この失敗した少数の者は不憫なものです。高位階級から拒絶され、低位階級からすら軽蔑される。彼らには多角形の学士のように訓練され成熟した能力もなければ、商人のように柔軟な応用力もない。公職や専門職への道は閉ざされていて、ときには結婚することすら難しくなってしまう。
過去の反乱や騒動のリーダーは、多くの場合は高位階級になりそこなった者から出ている。その被害はひどいものなので、進歩的な政治家の中には、大学の最終試験に落ちた者は全員、一生閉じ込めておくか苦痛をともなわない死刑に処す法律を作るべきという者もいる。その弾圧こそが本当の慈悲だ、というのが彼らの意見だ。
ちょっと話題はそれてしまったけど、不正規の形をした図形たちについても話しておかなくてはね。これはとても興味深いことなので、この次に話していくことにしよう。

『フラットランド―二次元の世界から多次元の冒険へ』
エドウィン・アボット・アボット(著) 牧野内 大史 (翻訳)
つづく… 第7章 フラットランドの不正規図形
自分を変える旅から、自分に還る旅へ。










